关键词:钢混组合梁;截面参数;优化;应力;敏感性;成桥状态;
作者简介:涂光亚,男,博士,副教授;
基金:国家自然科学基金资助项目(编号:51678068,51878074);
钢混组合梁斜拉桥主梁为钢结构,桥面系为混凝土结构,两者通过连接件结合在一起,共同受力,充分发挥了钢与混凝土两种材料的力学性能[1]。大跨度桥梁施工控制的主要目的,就是为了保证桥梁的施工安全以及成桥后主梁的线形和受力状态均满足设计要求[2]。关于组合梁斜拉桥受力性能的优化,最常见的方式是通过索力进行优化。肖汝诚、王永安、杨吉新、简伟峰等通过影响矩阵来确定成桥状态下的合理索力,施工阶段的索力优化和成桥后的索力调整[3,4,5];范立础[6]将结构弯矩当成控制目标;王程[7]、彭孝良[8]、张紫辰[9]基于弯曲能量法;刘军[10]采用未知荷载系数法;施乐[11]基于1阶优化算法均得到了成桥的最优索力。对于最优的索力所确定的成桥状态也可能会出现主梁局部应力较大的现象,而再次调索较为繁琐。郭超、火东存、储森森采用变主梁截面参数的方式优化组合梁应力[12,13,14]。该文对钢主梁截面参数成桥状态组合梁应力敏感性进行分析,利用钢主梁参数调整的方法,局部优化主梁的应力,作为对其合理成桥状态计算方法的补充。
1 工程概况
赤壁长江公路大桥主跨为720 m的双塔对称钢混组合梁斜拉桥。主桥共116对高强平行钢丝斜拉索,最大长度达387.18 m, 拉索间距为12 m和8 m两种形式,按照双索面扇形布置。主塔采用H形塔,桥型立面布置如图1所示。主桥为半漂浮体系,采用受力满足要求的双边箱截面钢主梁,主梁横断面如图2所示。钢主梁采用Q420D钢材,桥面板采用C60混凝土。钢主梁底板既变宽又变厚,宽度为2 450~3 200 mm, 厚度为32~70 mm。混凝土桥面板标准段厚度采用26 cm, 边跨桥面板加厚至59 cm(具有压重的作用),模型中成桥索力如表1所示。
2 有限元模型
采用BDCMS软件建立赤壁长江公路大桥主桥平面杆系有限元模型。斜拉索单元采用两端带刚臂的悬链线索单元模拟,主塔采用梁单元模拟,组合梁采用双层梁单元进行模拟如图3所示,上下两单元间采用刚臂相连。所有梁段的支架单元类型为一般桁架单元。同时为了方便读取斜拉索索力,在建模时将相同梁段上的一对斜拉索作为一个拉索单元。主梁及桥面板自重以均布荷载方式施加,全桥共划分843个节点,1 682个单元,其中塔墩186个单元,斜拉索116个单元,钢混组合梁1 380个单元。单元编号1~690为钢主梁,691~1 380为桥面板。计算模型共分为23个大工况,每个大工况包含若干个小工况,包含施工阶段和成桥运营阶段。在施工阶段中荷载主要考虑结构恒载,施工中的临时荷载,斜拉索张拉力和混凝土收缩徐变等。
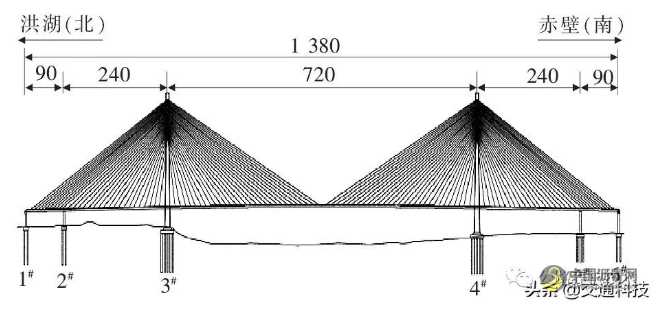
图1 赤壁长江公路大桥主桥立面布置图(单位:m)
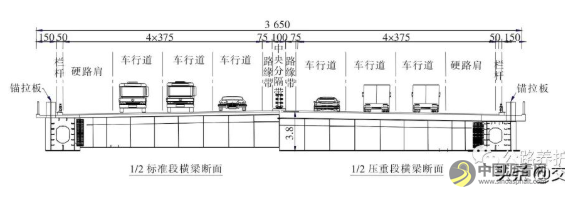
图2 赤壁长江公路大桥标准段断面图 (单位:cm)
表1 成桥索力
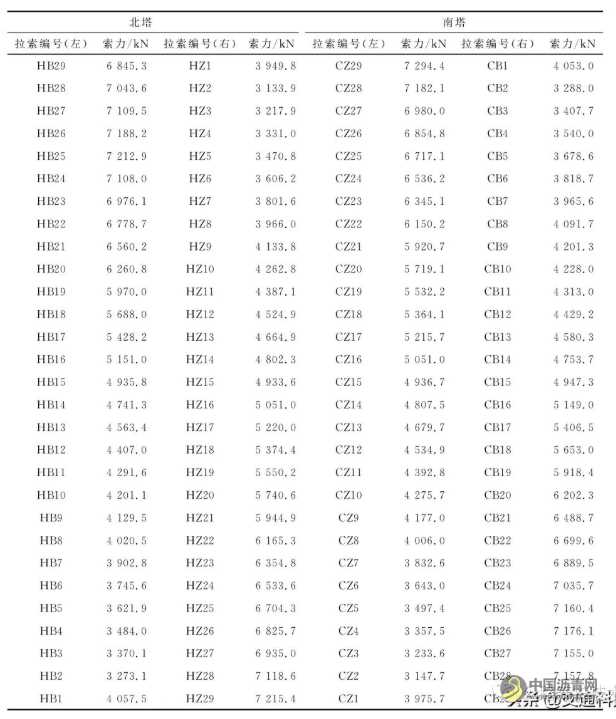
表1 成桥索力
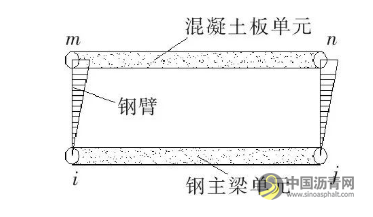
图3 双层梁单元模拟
3 研究思路
由于混凝土收缩徐变效应的影响,组合截面的应力和应变随时间而发生改变。建立BDCMS及Midas/Civil模型,以不改变钢主梁的横截面积为前提,对刚成桥及混凝土收缩徐变完成两种状态下的钢主梁截面参数均进行研究分析。以赤壁长江公路大桥塔区五段梁为研究对象,塔区五段主梁原截面顶板厚24 mm、宽2 600 mm、底板厚60 mm、宽3 000 mm, 腹板厚24 mm、高3 157 mm。调整塔区五段梁的钢主梁顶、底、腹板厚度,分析成桥状态下组合梁的受力性能。具体采用以下两种方案:
(1)钢主梁顶板加厚4mm,底板减薄3.5mm。
(2)腹板加厚2mm,顶板、底板均减薄2.3mm。
分析顶底板、腹板厚度变化对成桥状态下组合梁应力所产生的影响,得出对组合梁应力较为敏感的钢主梁截面参数,并采用Midas/Civil全桥模型进行局部优化。
4 刚成桥状态改变塔区主梁顶底板厚的受力分析
参数修改前后的主梁截面几何特性如表2所示。
表2 修改截面前后塔区主梁截面几何特性对照
| 单位 | 原截面 | 改截面 |
| m2 | 0.93 | 0.93 |
| m4 | 1.48 | 1.53 |
| m3 | 0.72 | 0.77 |
| m3 | 1.24 | 1.21 |
| m | 2.04 | 1.98 |
| m | 1.20 | 1.27 |
4.1 组合梁轴力分析
图4为修改截面前后主梁总轴力差值。
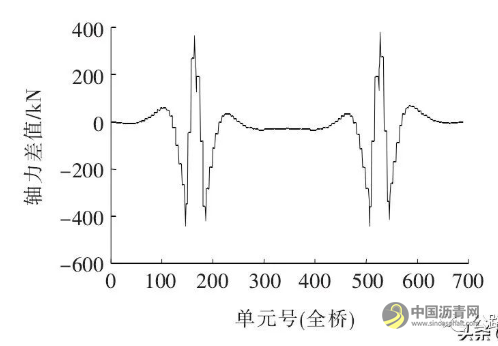
图4 改模型前后主梁总轴力差值
由图4可知:在刚成桥状态下改变顶底板厚全桥总轴力最大改变400 kN,占原桥总轴力的0.2%,说明改变顶底板厚对组合梁总轴力基本无影响。
图5为修改截面前后塔区主梁及桥面板轴力差值。
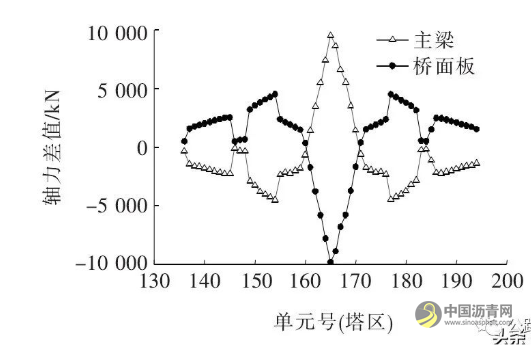
图5 改模型前后塔区主梁及桥面板轴力差值
由图5可知:① 虽然改变顶底板厚对组合梁总轴力无影响,但对组合梁轴力分配会产生影响。对于钢主梁,轴力最大增加了9 547 kN,增幅为9%,对于桥面板,轴力最大减小9 795 kN,减幅为8%;② 该影响对塔区梁段较为显著,对远离塔区梁段基本无影响。根据以上数据分析可知:平均顶底板厚增减1 mm, 塔区梁段钢主梁轴力最大可增加2%,桥面板轴力最大可减小2%。
4.2 组合梁弯矩分析
由于桥面板厚度相对于整个主梁的高度很小,所以桥面主要承受轴力,基本不承受弯矩,经计算分析桥面板所受弯矩只占截面总弯矩的1%,因此可以认为组合梁总弯矩是由钢主梁所决定的,钢主梁的弯矩变化规律即组合梁弯矩的变化规律。图6为修改模型前后塔区钢主梁弯矩差值。
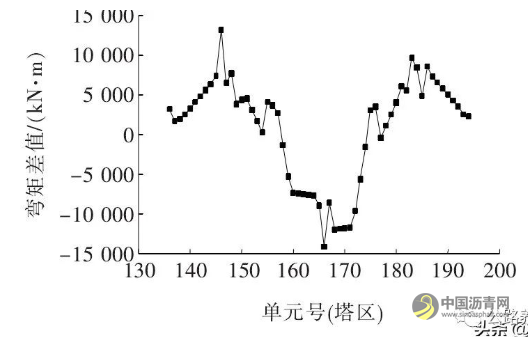
图6 改模型前后塔区钢主梁弯矩差值
由图6可知:主梁弯矩变化分为3个区间,塔区梁段负弯矩增大,两侧远离塔区梁段正弯矩增大。在塔区梁段弯矩变化幅度最大,达到14 100 kN·m, 说明顶板增厚,底板减薄对塔区梁段弯矩有很大影响。远离塔区梁段主梁正弯矩均略有增加,幅度不大。
4.3 钢主梁应力分析
图7为修改模型前后塔区钢主梁上下缘应力差值百分比。
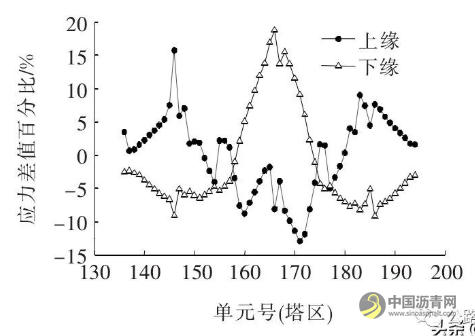
图7 改模型前后塔区钢主梁上下缘应力差值百分比
由图7可知:塔区附近梁段钢主梁上缘应力减小,下缘应力增大。上缘应力最大减小17.4 MPa, 减幅为13%,下缘应力最大增大21 MPa, 增幅为19%。主要原因为塔区梁段钢主梁轴力和弯矩均有增加,所以导致上、下缘应力有较大变化,这也为实现主梁应力优化提供了可能。塔区梁段两侧主梁上缘应力均增大,下缘应力均减小,左侧上缘应力最大增幅为16%,下缘最大减幅为9%。右侧上缘最大增幅为9%,下缘最大减幅为9%。塔区梁段钢主梁应力具体数据见表3。
表3 改变顶底板厚塔区梁段钢主梁上下缘应力对比/MPa
单元号 | 原上缘应力 | 改上缘应力 | 上缘应力差值 | 原下缘应力 | 改下缘应力 | 下缘应力差值 |
162 | -131.7 | -124.4 | 7.3 | -98.8 | -108.4 | -9.6 |
163 | -130.1 | -125.0 | 5.1 | -99.4 | -111.3 | -11.9 |
164 | -125.9 | -123.0 | 2.9 | -101.8 | -115.9 | -14.1 |
165 | -123.8 | -121.6 | 2.2 | -103.4 | -120.9 | -17.5 |
166 | -109.0 | -100.2 | 8.8 | -111.7 | -132.7 | -21.0 |
167 | -123.0 | -118.2 | 4.8 | -102.5 | -116.6 | -14.1 |
168 | -125.8 | -115.3 | 10.5 | -100.4 | -116.0 | -15.6 |
169 | -131.0 | -118.1 | 12.9 | -96.9 | -110.2 | -13.3 |
170 | -133.6 | -118.4 | 15.2 | -95.3 | -106.3 | -11.0 |
171 | -134.7 | -117.3 | 17.4 | -95.0 | -103.7 | -8.7 |
172 | -133.2 | -117.4 | 15.8 | -96.4 | -102.3 | -5.9 |
4.4 桥面板应力分析
桥面板弯矩很小,其应力主要由轴力所决定。图8为修改模型前后塔区桥面板上下缘应力差值百分比。
由图8可知:桥面板上下缘应力变化规律基本一致,故仅分析桥面板上缘应力。塔区梁段上缘应力减小,最大减小1.2 MPa, 减幅为9.2%,远离塔区梁段上缘应力均增大,但幅度较小。由以上分析可知顶底板增减1 mm其上缘应力最大变化幅度为2.3%。
5 刚成桥状态改变塔区主梁腹板厚的受力分析
参数修改前后的主梁截面特性如表4所示。
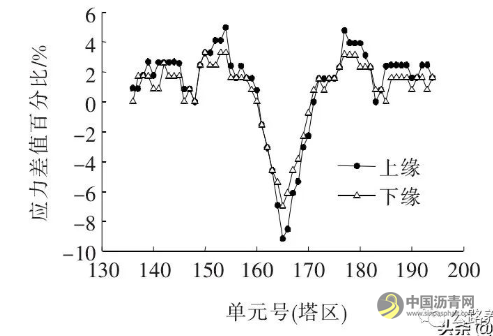
图8 改模型前后塔区桥面板应力差值百分比对比
表4 改模型前后塔区主梁截面特性对照
| 单位 | 原截面 | 改截面 |
| m2 | 0.93 | 0.93 |
| m4 | 1.48 | 1.44 |
| m3 | 0.72 | 0.70 |
| m3 | 1.24 | 1.20 |
| m | 2.04 | 2.04 |
| m | 1.20 | 1.20 |
5.1 组合梁轴力分析
图9为修改模型前后塔区主梁总轴力差值。
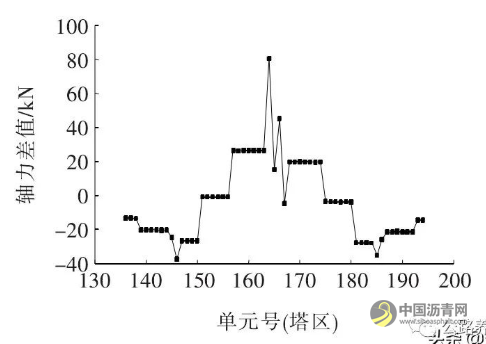
图9 改模型前后塔区主梁总轴力差值
由图9可知:腹板增厚2 mm, 塔区主梁总轴力差值百分比小于0.04%,平均腹板增厚1 mm, 主梁总轴力最大改变小于0.02%,说明改变腹板厚对总轴力变化基本无影响。
图10为修改模型前后塔区主梁及桥面板轴力差值。
由图10可知:腹板增厚2 mm, 主梁轴力最大改变1 314 kN,增幅为1.27%,桥面板轴力最大改变1 330 kN,减幅为1.08%。平均腹板增厚1 mm, 主梁轴力最大改变幅度仅为0.6%,桥面板为0.5%,说明变腹板厚对组合梁轴力分配的影响也很小。
5.2 组合梁弯矩分析
图11为修改模型前后塔区钢主梁弯矩差值。
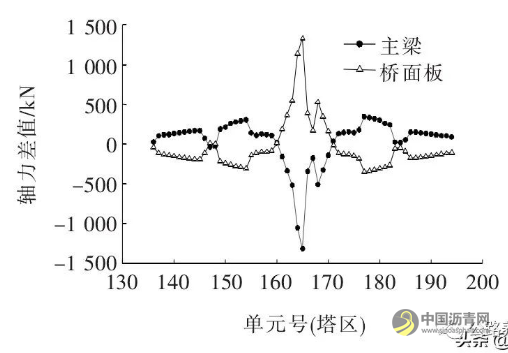
图10 改模型前后塔区主梁及桥面板轴力差值
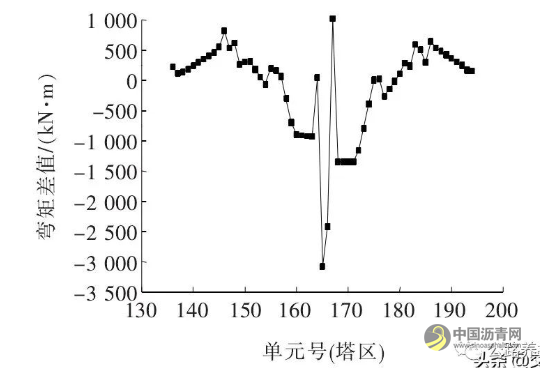
图11 改模型前后塔区钢主梁弯矩差值
由图11可知:腹板每增厚1 mm, 塔区梁段弯矩最大可减小1 500 kN·m, 平均减小350 kN·m。结合图6、图11可以看出:腹板增厚1 mm, 其对弯矩的影响效率远小于顶、底板增减1 mm。
5.3 钢主梁应力分析
图12为修改模型前后塔区钢主梁上下缘应力差值百分比。
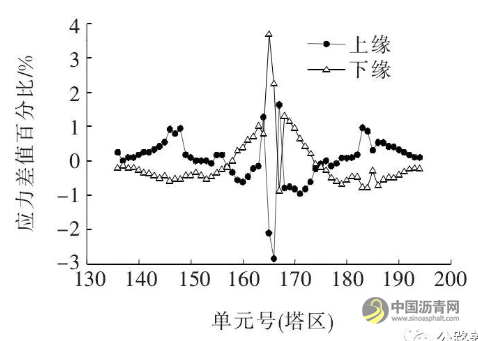
图12 改模型前后塔区钢主梁上下缘应力差值百分比
由图12可知:塔区梁段钢主梁上缘应力减小,下缘应力增大。上缘应力最大减幅为2.8%,下缘最大增幅为3.6%,即腹板增厚1 mm, 塔区主梁上缘应力最大减小1.4%,下缘最大增加1.8%。远离塔区梁段主梁上缘应力均增大,下缘应力均减小,其上下缘应力最大变化幅度为1%。即腹板增厚1 mm, 对0#块两侧上下缘应力最大变化幅度为0.5%,以上分析表明腹板增厚对塔区主梁应力有一定程度影响,但其应力改变效率远小于改变顶底板厚的应力改变效率。
5.4 桥面板应力分析
图13为修改模型前后塔区桥面板上缘应力差值百分比。
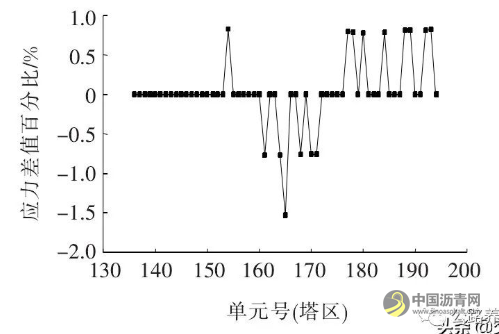
图13 改模型前后塔区桥面板上缘应力差值百分比
由图13可知:腹板增厚1 mm, 桥面板上缘应力最大变化幅度为0.7%,说明改变腹板厚对塔区桥面板应力影响很小。
6 收缩徐变完成改变塔区主梁顶底板厚的应力分析
6.1 钢主梁应力分析
图14为修改模型前后塔区钢主梁上下缘应力差值百分比。
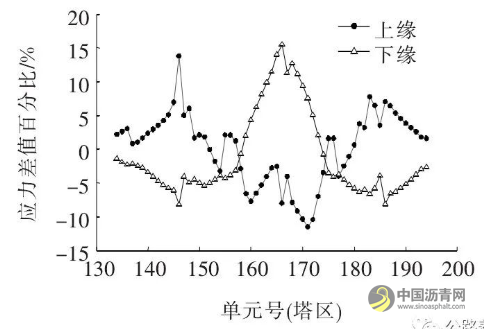
图14 改模型前后塔区钢主梁上下缘应力差值百分比
由图14可得:塔区梁段钢主梁上缘应力减小,最大减小17.2 MPa, 减幅为11.5%。钢主梁下缘应力增大,最大增大21.3 MPa, 增幅为15.5%。远离塔区主梁上缘应力均增大,下缘应力均减小,其上缘最大变化幅度为13%,下缘为8%。
改变钢主梁顶底板厚度,对截面应力的分布影响较大。结合图7与图14可知:刚成桥与混凝土收缩徐变完成两种状态下,改变塔区顶底板厚,对塔区主梁上下缘应力的数值影响基本相同。
6.2 桥面板应力分析
图15为修改模型前后塔区桥面板上下缘应力差值百分比。
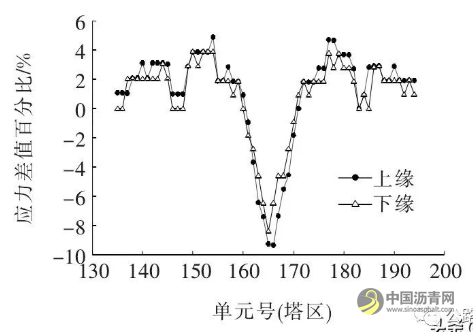
图15 改模型前后塔区桥面板上下缘应力差值百分比
由图15可知:混凝土收缩徐变完成后,改变钢主梁顶底板厚,桥面板上下缘应力是同步发生变化的,与刚成桥状态下的变化规律一致。
图16为修改模型前后塔区桥面板上缘应力对比。
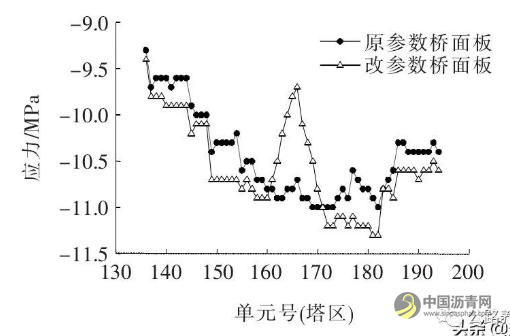
图16 改模型前后塔区桥面板上缘应力对比
由图16可知:塔区桥面板上缘压应力最大减小1 MPa, 最大减幅为9.3%。顶底板增减1 mm, 桥面板上缘压应力最大减小0.25 MPa, 减幅为2.3%。结合图8可知:刚成桥状态下桥面板上缘应力最大减小1.2 MPa, 最大减幅为9.2%。说明改变钢主梁顶底板厚对两种状态下桥面板应力影响均较大。
7 优化前后组合梁应力对比
采用Midas/Civil建立全桥模型,作一次成桥计算,按设计要求考虑结构自重并施加二期恒载,分别设置车道荷载与车辆荷载,按六车道进行布载并进行横向折减。偏载系数设定为1.15,温度荷载考虑整体升温与整体降温以及梯度温度上升、下降。采用标准组合即所有作用的分项系数取1.0进行截面应力分析。
针对刚成桥状态下Midas/Civil模型中塔区及辅助墩主梁下缘压应力局部偏大,而上缘应力富余度较大,边墩桥面板由于支座模拟出现少许拉应力的情况,均采用增厚底板,减薄顶板的方法进行局部优化,作为对该成桥状态计算方法的补充。
在原模型标准组合作用下,边墩桥面板上、下缘最大应力分别为3.2、3.0 MPa。图17、18为模型优化前后全桥桥面板上下缘应力差值。
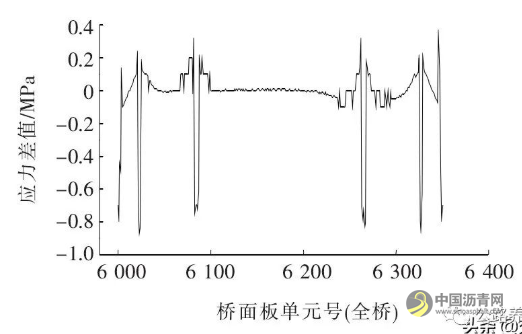
图17 模型优化前后桥面板上缘应力差值
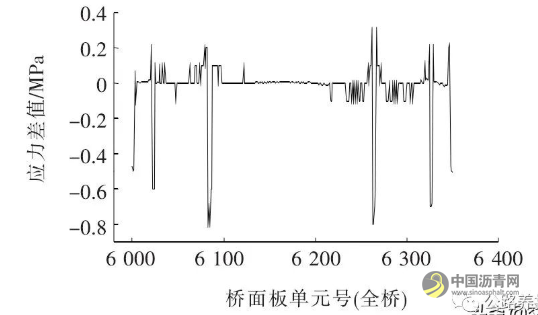
图18 模型优化前后桥面板下缘应力差值
由图17、18可知:优化后边墩桥面板上下缘拉应力最大降至2.6 MPa。辅助墩及塔区压应力最大增大0.85 MPa。
以洪湖侧主梁为例,主梁上缘最大压应力为120 MPa, 下缘最大为145 MPa, 故采取底板增厚4 mm的方法。图19、20为模型优化前后全桥钢主梁上下缘应力差值。
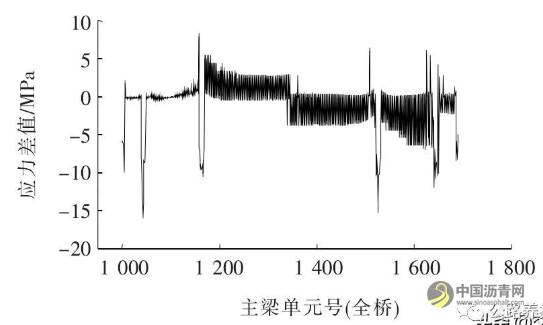
图19 模型优化前后钢主梁上缘应力差值
由图19、20可知:优化后塔区钢主梁下缘压应力最大减小15 MPa, 上缘压应力增大15 MPa, 对不改变主梁参数区域应力影响较小,基本达到期望值。
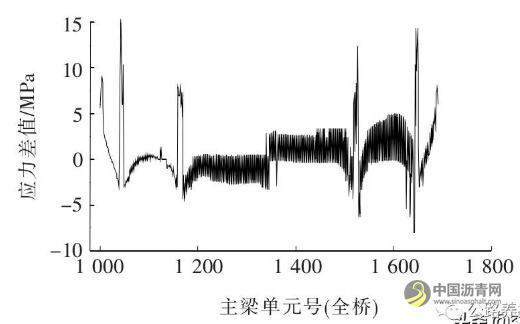
图20 模型优化前后钢主梁下缘应力差值
8 结论
以赤壁长江大桥为工程背景,分析在成桥索力一定条件下,改变塔区钢主梁截面参数对成桥状态组合梁的应力敏感性进行分析,所得结论如下:
(1) 改变塔区主梁截面参数,其内力影响主要集中在塔区,对塔区梁段两侧影响较小。变顶底板厚对组合梁总轴力无影响,对塔区梁段钢主梁与桥面板的轴力分配会产生较大的影响。
(2) 桥面板弯矩很小,组合梁弯矩由钢主梁所决定,顶板增厚或底板减薄两种方式均可改变塔区梁段弯矩。改变塔区梁段顶底板厚对塔区钢主梁上下缘应力影响明显,故通过改变主梁截面参数改善组合梁局部应力可行。
(3) 改变腹板厚对组合梁内力影响均较小,故对钢混组合梁局部应力优化应尽量不调腹板,以调顶底板参数更为合理。
(4) 改变钢主梁顶底板厚在刚成桥和收缩徐变完成两个状态下对主梁及桥面板的内力应力均敏感。
针对成桥状态下Midas/Civil模型中塔区及辅助墩主梁下缘压应力局部偏大,而上缘压应力相对较小,边墩桥面板上下缘拉应力较大的情况,采用钢主梁参数调整的方法进行局部优化,作为对该索力下成桥状态计算方法的补充,基本达到了期望值。
参考文献
[1] 赵雷,孙才志,陈文元.大跨度结合梁斜拉桥的参数敏感性分析[J].世界桥梁,2011(6):38-41.
[2] 肖雄,黄志霜.大跨度叠合梁斜拉桥施工控制参数敏感性分析[J].四川建筑,2016,36(5):117-119,121.
[3] 肖汝诚.确定大跨径桥梁结构合理设计状态的理论与方法研究[D].同济大学博士学位论文,1996.
[4] 王永安,刘世同,谭红梅,等.斜拉桥索力优化理论研究[J].公路,2006,51(5):31-34.
[5] 杨吉新,张朝,吴爱平,等.基于影响矩阵法的S形曲线斜拉桥索力优化[J].工程与建设,2020,34(2):234-236.
[6] 范立础,杜国华.斜拉桥索力优化及非线性理想倒退分析[J].重庆交通学院学报,1992,11(3):1-13.
[7] 王程,尹超.弯曲能量最小法在组合梁斜拉桥设计中的应用[J].工程与建设,2017,31(5):671-673.
[8] 彭孝良,单成林.组合梁斜拉桥合理成桥状态确定方法对比分析[J].低温建筑技术,2018,40(6):45-49.
[9] 张紫辰.钢—混组合梁(塔)斜拉桥设计参数优化研究[D].兰州交通大学硕士学位论文,2018.
[10] 刘军.基于未知荷载系数法的斜拉桥索力优化[J].交通科技,2020(4):6-9,14.
[11] 施乐.基于一阶优化算法的钢-混组合梁恒载索力优化[J].工程与建设,2017,31(1):20-23.
[12] 郭超.钢-混凝土组合梁应力分析及截面优化研究[D].长沙理工大学硕士学位论文,2013.
[13] 火东存,段运.组合梁截面尺寸优化分析[J].四川建材,2018,44(4):149-150.
[14] 储森森.公路钢—混凝土连续组合梁桥的截面优化设计研究[D].合肥工业大学硕士学位论文,2018.
[15] 张德平,周健鸿,王东晖.赤壁长江公路大桥主桥主梁设计[J].桥梁建设,2019,49(4):81-85.
[16] 杨胜.钢混结合梁大边跨连续箱梁桥总体设计[J].中外公路,2019,39(2):165-168.